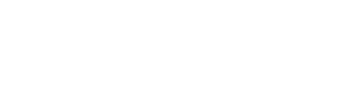Завдання на рух зарядженої частинки в електричному полі - зустрічаються на іспитах досить часто. Це, як правило, комбіновані завдання, для вирішення яких необхідно використовувати кінематичні і динамічні формули. Також рішення таких задач не обходиться без знання формули сили Кулона і вміння розв'язувати системи рівнянь. Для того, щоб вирішувати завдання на рух зарядженої частинки в електричному полі, можна використовувати алгоритм, з яким я пропоную ознайомитися нижче.
Погляньмо на цей алгоритм на прикладі рішення наступної задачі.
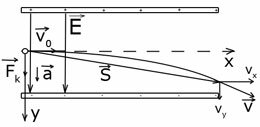
Позитивно заряджена частинка влітає в простір між пластинами плоского повітряного конденсатора, з початковою швидкістю v0, спрямованої паралельно пластинам. Напруженість електричного поля Е, відстань між пластинами конденсатора d. Визначити зміщення зарядженої частинки по вертикалі.
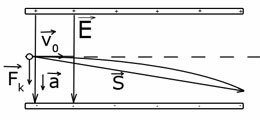
- Для початку необхідно зробити хороший малюнок (НЕ мікроскопічний). На малюнку вказуємо початкові характеристики (початкову швидкість, її напрямок, полярність пластин конденсатора, напрямок вектора напруженості електричного поля)
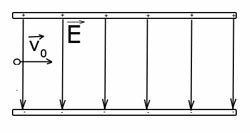
- На будь-який заряджене тіло (частку) з боку електричного поля діє сила Кулона, напрямок цієї сили визначається чисто математично (якщо частка має позитивний заряд, то напрямок сили Кулона збігається з напрямком вектора напруженості електричного поля, якщо частка має негативний заряд - то напрям сили і вектора напруженості електричного поля - протилежні одна одній). Визначивши напрямок сили Кулона, вказуємо напрямок вектора прискорення, що повідомляється зарядженої частинки силою Кулона. Напрямок сили Кулона і вектора прискорення завжди збігаються!
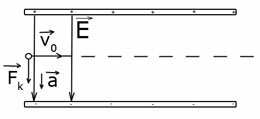З цих рівнянь визначаємо прискорення зарядженої частинки в електричному полі.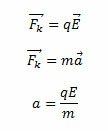 
- зображуємо траєкторію руху частинки. Оскільки на заряджену частинку діє одна сила, і напрямок вектора швидкості і вектора прискорення взаємно перпендикулярні один одному, траєкторія руху являє собою параболу (в межах конденсатора)
- Зобразимо вектор переміщення частинки в полі конденсатора. Записуємо кінематичні формули для визначення переміщення або швидкості тіла для рівноприскореного руху
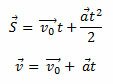
- Вибираємо зручне напрямок координатних осей
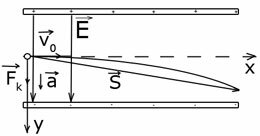
- Записуємо кінематичні рівняння в проекціях на вибрані осі. Важливо! Проекція вектора переміщення на вісь ох чисельно дорівнює довжині пластин конденсатора, а проекція вектора переміщення на вісь ОY чисельно дорівнює зсуву зарядженої частинки по вертикалі.
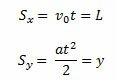
- Вирішуємо отриману систему рівнянь щодо невідомих величин.
- Якщо в питанні до задачі мова йде про швидкість зарядженої частинки після вильоту з конденсатора (напрямку вектора швидкості в якийсь момент часу), то на малюнку зображуємо вектор швидкості і визначаємо його компоненти. А далі визначаємо невідому величину.
Як видно з алгоритму, рішення задач на рух частинки в електричному полі конденсатора, не представляє особливої складності. Треба лише послідовно виконувати ті дії, які описані вище. І бути уважними.
Ви можете Залишити коментар , Або поставити трекбек зі свого сайту.